В неспокойной атмосфере

§ 3.1. ПЕРЕДАТОЧНЫЕ И ПЕРЕХОДНЫЕ ФУНКЦИИ
ДЛЯ ПАРАМЕТРОВ ПРОДОЛЬНОГО ДВИЖЕНИЯ
ПРИ ВОЗДЕЙСТВИИ ВЕТРА

Основной задачей данного параграфа является получение и анализ передаточных функций для параметров продольного дви­жения самолета в неспокойной атмосфере. В последующих пара­графах этой главы передаточные функции используются для получения на основании соотношений (2.46) и (2.47) характери­стик продольного движения в турбулентной атмосфере.

Переходные функции продольного движения, рассматривае­мые совместно с передаточными функциями, дают наглядное представление о поведении самолета при попадании в одиночный порыв ветра вида единичной ступенчатой функции. Хотя таких порывов в реальной атмосфере не существует, однако встречают­ся порывы с большим градиентом, которые в первые секунды их воздействия на самолет можно считать близкими к ступенчатым.

В данной главе произведено сравнение динамики самолета с зажатыми рулями и при управлении автопилотом. Исследова­ние поведения самолета с зажатыми рулями представляет не только теоретический, но и практический интерес, поскольку инст­рукции рекомендуют летчику при полете в неспокойной атмос­фере по возможности не вмешиваться в управление самолетом, удерживая рули в определенном положении. Однако все чаще для управления самолетом в этих условиях используется автопилот.

Оценим роль продольной и нормальной составляющих скоро­сти ветра в возмущении параметров продольного движения. Для этого рассмотрим передаточные и переходные функции самолета с зажатым рулем высоты и самолета, управляемого автопилотом с высотным корректором [закон (2.13)] и без него [закон (2.14)].

На основании полной системы уравнений (2.10), справедливой для горизонтального полета самолета с зажатым рулем высоты, получаем следующие передаточные функции при воздействии горизонтальной составляющей ветра.

Для угла тангажа [16]

Отрицательный знак передаточной функции (3.1) указывает на то, что в первый момент после попадания в попутный поток воздуха постоянной скорости (№*>0) самолет опускает нос (ДО<0). В установившемся режиме (р = 0) приращение угла тангажа становится равным нулю.

(п) — С(р) = С»Р* — г схР7 + сгР + а* К Л(р) А(р)

Для приращения скорости по связанной оси х

Вид передаточных функций (3.3) — (3.6) позволяют утверждать, что в установившемся режиме (р=0) при воздействии постоян­ного ветра Wx приращения параметров Vgv, yg, пх и пу равно нулю.

Передаточные функции для самолета с зажатым рулем высо­ты при воздействии вертикальной составляющей ветра имеют следующий вид.

Для угла тангажа

WtnWy(p)=-

Отрицательный знак передаточной функции (3.7) указывает на то, что в первый момент после попадания в восходящий поток постоянной скорости (Wv>0) устойчивый самолет опускает нос вниз («клюет на ветер»). В установившемся режиме (р=0) при

$,грйд

а)

6)

Л)

 

постоянной скорости вертикального ветра приращение угла тан* гажа равно нулю.

Для приращения скорости по связанной оси х

goP[17] [18] + gP2 + giP
А(р)

•Для скорости по связанной оси у

Wv ( Р)_____ Шр} крр3 + ht р2 + h$p + at

А(р) А(р)

Щля вертикальной скорости самолета (в земных осях)

WyJw (р) = ■1 (р)- = *■ р2 +hP + а*

Vу А(р) А(р)

Свободные члены числителей и знаменателей (3.9) и (3.10) совпадают, что указывает на то, что в установившемся режиме вертикальная скорость самолета будет равна скорости постоян­ного по величине ветра Wy.

Для горизонтальной перегрузки

WnxMy(p)= j-WbVgx/V)y(p). (3.11)

Для вертикальной перегрузки

w-r*,(P) = ywi’l,,(Pl — (3.12)

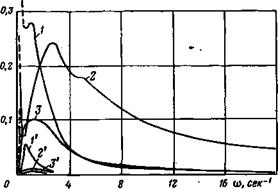
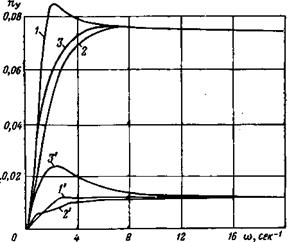
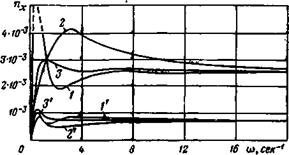
На рис. 3.1 в качестве примеров приведены амплитудно-час­тотные характеристики для практически наиболее важных пара­метров продольного движения тяжелого транспортного самолета в крейсерском режиме полета (ниже для краткости этот самолет будем называть самолетом № 1). Эти характеристики построены по рассмотренным выше передаточным функциям для угла тан­гажа, вертикальной и горизонтальной перегрузок при действии вертикальной (кривые 1) и горизонтальной (кривые 1′) состав­ляющих ветра. Начальные участки этих же характеристик в бо­лее крупном масштабе для о показаны на рис. 3.2 (кривые /). На рис. 3.2 характеристики самолета построены только при воз­действии вертикальной составляющей ветра, так как графики на рис. 3.1 показывают, что угол тангажа и вертикальная перегрузка

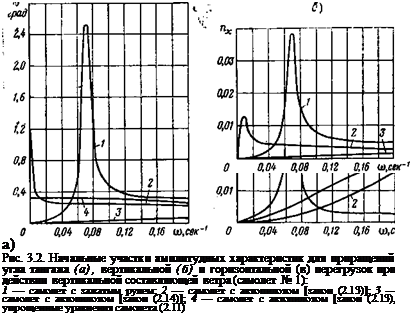при воздействии горизонтальной составляющей ветра примерно на порядок меньше, чем от вертикальной. Несколько больше роль горизонтальной составляющей в создании горизонтальной пере­грузки (рис. 3.1,в), но последняя по абсолютной величине мала и в большинстве случаев практически не представляет интереса. На основании этого ниже, как правило, будет анализироваться поведение самолета под действием вертикальных порывов ветра.

В)

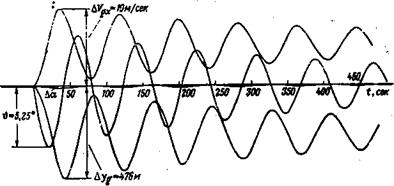
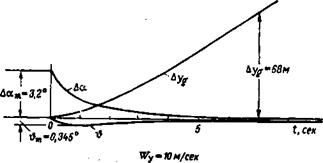
Графики на рис. 3.2 показывают, что на очень низких часто­тах характеристики самолета с зажатыми рулями содержат пи л значительной амплитуды, обусловленный длиннопериодически!’ движением (фугоиды). Это обстоятельство хорошо подтверж дается переходными процессами, соответствующими входу само лета № 1 в вертикальный поток воздуха, имеющий скорость Г„=10 м/сек (рис. 3.3).

Необходимо обратить внимание на то, что приращение угла атаки Да, вызванное вертикальным порывом ветра, уменьшается

практически до нуля за время короткопериодического движения и не возмущается в процессе фугоидных колебаний. Переходная функция для угла атаки практически совпадает с переходной функцией для вертикальной перегрузки. Поэтому при анализе продольного движения главным образом с точки зрения перегру­зок, испытываемых самолетом, можно ограничиться боЛее про-

Рис. 3.3. Переходные процессы самолета № 1 с зажатым рулем, полученные по полным уравнениям (2.10), при воздействии вертикального ветра

стыми уравнениями (2.11). Ниже будет показано, что для само­лета с автопилотом без высотного корректора такое допущение тем более справедливо, так как автопилот уничтожает фугоидные

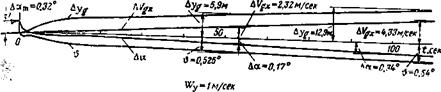
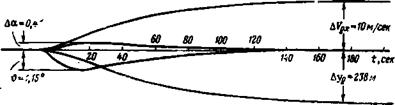
Рис. 3.4. Переходные процессы самолета 1 с зажатым рулем, полу­ченные по полным уравнениям (2.10), при воздействии горизонтального ветра

колебания, и переходные характеристики, получаемые по полным

(2.10) и упрощенным (2.11) уравнениям, совпадают лучше, чем у самолета без автопилота.

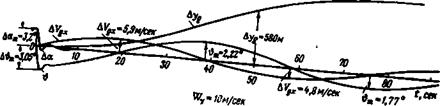
На рис. 3.4 приведены переходные процессы для самолета № і с зажатым рулем, соответствующие входу самолета в попут­ный поток воздуха, имеющий скорость И7*=10 м/сек. Чтобы бо — лее наглядно представить фугоидные колебания, масштаб вре­мени уменьшен. Переходные процессы на рис. 3.4 показывают, что

у самолета с зажатым рулем при попадании, в горизонтальным порыв угол атаки почти не возмущается, а приращения угла тан­гажа, путевой скорости и высоты совершают слабо затухающи, колебания с большим периодом. При этом колебания скорости і. высоты полета совершаются относительно значений этих величні і в новом установившемся режиме.

Получим передаточные функции для параметров движени:; самолета с зажатыми рулями при воздействии горизонтальної: составляющей ветра на основе более, простых уравнений (2.11)

Для угла тангажа *

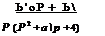
W*!Wx(p)=

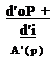Для скорости по связанной оси у

W»yI[19]x(P) = — JWygl*JP)-

hP +’а’* А’(р)

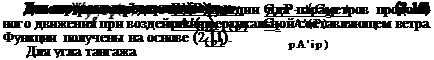Для вертикальной скорости самолета

Для вертикальной скорости самолета

Для вертикальной перегрузки

(3.20)

Найдем также передаточную функцию для дополнительной перегрузки, вызываемой угловыми движениями самолета, т. е. его колебаниями относительно центра тяжести. Эту перегрузку опре­делим лишь для случая вертикальной составляющей ветра. Пере­даточная функция для перегрузки на плече I от центра тяжести, вызываемой угловыми движениями, имеет вид

(3.21)

Плечо / имеет положительный знак для точек, расположенных от центра тяжести к хвосту самолета.

Необходимо отметить, что передаточные функции (3.13) и

(3.15) не могут быть использованы для расчета движения само­лета при действии случайного ветра, так как они содержат чисто интегрирующее звено в качестве множителя. Это обстоятельство приведет к бесконечно большим значениям дисперсии угла тан­гажа и вертикальной скорости при воздействии случайного ветра. Такой результат является следствием пренебрежения изменением скорости полета. Передаточные функции (3.1) и (3.4) для тех же параметров, но полученные по полным уравнениям (2.10), лише­ны указанного недостатка.

Частотные характеристики для угла тангажа и перегрузки, полученные на основании упрощенных формул, практически со­впадают с теми, которые приведены на рис. 3.1, а и б (кривые 1 и 1′). Это подтверждает высказанное выше утверждение о том, что короткопериодическое движение самолета без автопилота при воздействии ветра достаточно хорошо описывается системой уравнений (2.11).

В частотных характеристиках, полученных по упрощенным уравнениям, исчезают пики на малых частотах (рис. 3.2,а и в), соответствующие фугоидам. Однако площадь этих пиков ничтож­на и, следовательно, ничтожна их роль при определении диспер­сии угла тангажа и перегрузки при воздействии на самолет слу­чайного ветра. Для иллюстрации всех этих положений рассмот­рим переходные. процессы самолета № 1, полученные по Уравнениям (2.11). Эти функции соответствуют входу самолета в вертикальный ветер №=10 м/сек (рис. 3.5). Сравнение рис. 3.5 с рис. 3.3 показывает, что в пределах времени затухания корот­копериодического движения процессы на обоих рисунках близки друг к другу.

Перейдем к анализу передаточных и переходных функций с автопилотом. Объединяя уравнения самолета (2.10) и автопилота с законом управления (2.13), получаем передаточные функции Для параметров продольного движения.

При воздействии горизонтальной составляющей ветра этг: функции имеют следующий вид.

Для угла тангажа *

W[20],Wx(p) =

Лр) ____________________ JoP3 + J’lP2 + hP________ /3 22

КІР) Pi + k{p* + k2p> +k3p2 + k4p-г kS ’

Для горизонтальной перегрузки

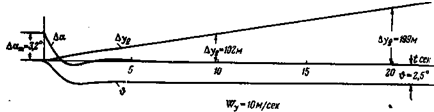
.(3.23,

Для вертикальной перегрузки

Wn lw (р)=~— =-— т°рЬ + щр*+ щр3 ■ (3.24

‘У9*’" g К(р) g К(р) У

Передаточные функции при воздействии вертикальной состав­ляющей ветра имеют следующий вид.

Для угла тангажа

w, lw («)= ”i£L= _ ЪР + ЪР^ + ър + п, (3 25) 1 уКУ К(Р) Kip)

Для горизонтальной перегрузки

w /-Ч 1 Qip) _ 1 ЯоРь + Я1Р*+Я2Р3 + ЯзР2 + 94Р /326)

g КІР) g КІР)

Для вертикальной перегрузки

,«,(/>)=-LA(3.27)

y’ yK g кІР) g Kip) v

Амплитудно-частотные характеристики, построенные на осно­вании передаточных функций[21] (3.22) — (3.27) для самолета № 1

приведены на рис. 3.1 (кривые 2 и 2′). Кривые 2 относятся к воз­действию вертикальной, а кривые 2′ — горизонтальной составля­ющих ветра. Для малых частот характеристики, относящиеся к вертикальному ветру, приведены на рис. 3.2 (кривые 2). Харак­теристики на рис. 3.2 показывают, что автопилот с законом управления (2.13) срезает пик фугоидных колебаний для верти­кальной перегрузки и уменьшает пик для горизонтальной пере­грузки. Неблагоприятным обстоятельством является смещение

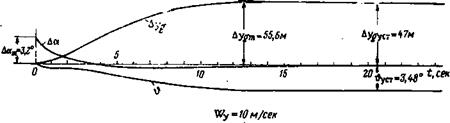
Рис. 3.6. Переходные процессы самолета № 1 с автопилотом [закон (2.13)], полученные по полным уравнениям (2.10), при воздействии вертикального ветра

пика на характеристике угла тангажа на нулевую частоту (рис. 3.2,а), в результате чего действие вертикального ветра при­водит к значительному отклонению всех параметров от их значе-

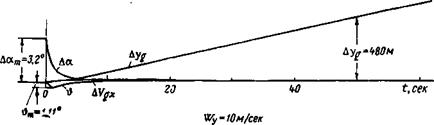
Рис. 3.7. Переходные процессы самолета № 1 с автопилотом [закон (2.13)], полученные по упрощенным уравнениям (2.11), при воздействии вертикаль­ного ветра

ний в установившемся режиме. На рис. 3.2, а приведена также амплитудно-частотная характеристика 4, построенная по упро­щенной передаточной функции, когда изменение скорости не учитывается [уравнения (2.11) и автопилот (2.13)]. В характери­стике 4 отсутствует пик на нулевой частоте, что очень существен­но влияет на динамику самолета.

Проиллюстрируем эти результаты с помощью переходных Функций для самолета № 1, представленных на рис. 3.6 и 3.7. Переходные функции на рис. 3.6 получены по полным уравнениям

(2.10) . Осциллограммы на рис. 3.6 указывают на очень неблаго­приятный характер переходного процесса у самолета с автопило­том, имеющим высотный корректор, при попадании в вертикаль­ный поток воздуха. Чтобы стабилизировать самолет на новой

высоте, при ветре, направленном, например, вверх, автопилот за­ставляет самолет опустить нос, вследствие чего увеличивается скорость полета. Для обеспечения равновесного режима при но­вом значении скорости нужно значительно уменьшить угол атаки. Вследствие малого значения передаточного числа автопилота по высоте (/„=0,07 град • руля/м) все эти нежелательные явления развиваются очень медленно. Поэтому в подавляющем большин­стве случаев самолет выйдет из зоны действия вертикального порыва раньше, чем указанные явления успеют развиться. Но и при кратковременном воздействии на самолет вертикальных по­рывов влияние высотного корректора будет отрицательным. К этому надо добавить, что в качестве датчика сигналов об изме­нении высоты в настоящее время используется барометрический прибор-статоскоп. Такой датчик работает удовлетворительно лишь в условиях спокойной атмосферы. В турбулентной атмос­фере наблюдаются пульсации давления, которые воспринимаются датчиком как колебания высоты полета. В этих условиях коррек­тор высоты может давать ложные и значительные по величине сигналы на автопилот, которые вызовут нежелательные эволю­ции самолета.

Второй особенностью рассматриваемого движения самолета с автопилотом, имеющим высотный корректор, при попадании в вертикальный поток воздуха является принципиальная невозмож­ность исследования этой задачи с помощью уравнений в откло­нениях (2.10), если скорости вертикального ветра значительны. В этом случае отклонения скорости и углы атаки от исходных значений получаются такими большими, что для исследования динамики полета необходимо использовать исходные нелинейные уравнения. Поэтому движение самолета, показанное на рис. 3.6, исследовалось при скорости ветра Н7„=1 м/сек. Даже при этом условии установившиеся значения отклонений параметров от их значений в невозмущенном режиме, вычисленные по приведенным выше передаточным функциям, получаются следующими:

Д0уст=-1,15°, Wgx=l7,5 м/сек, Дуг = 29

На рис. 3.6 эти значения не показаны, так как за время осцил- лографирования процесс не достиг установившегося состояния.

На рис. 3.7 приведены переходные процессы для того же слу­чая, но без учета изменения скорости полета (уравнения 2.11). Здесь значение скорости вертикального ветра принималось рав­ным 10 м/сек, так как в поведении системы самолет — автопилот нет никаких особенностей. Фугоидные колебания уничтожаются автопилотом, переходные процессы быстро заканчиваются, и са­молет продолжает полет с незначительным отклонением высоты.

Сравнение рис. 3.6 и 3.7 ясно показывает, что исследование динамики самолета с автопилотом, имеющим высотный коррек­тор, необходимо проводить с учетом изменения скорости.

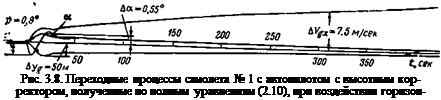
На рис. 3.8 приведены переходные процессы для самолета № 1 с автопилотом, имеющим высотный корректор, показываю­щие поведение самолета при попадании в попутный поток возду­ха №*=10 м/сек. Эти функции получены по полным уравнениям самолета (2.10). В этом случае не возникает таких больших от­клонений от исходного режима, как это имело. место при входе самолета с автопилотом, имеющим высотный корректор, в вер­тикальный поток воздуха (рис. 3.6). Однако процесс перехода к новому установившемуся режиму, также весьма затянут и состав­ляет в рассматриваемом примере около 10 мин.

Вследствие установленного выше отрицательного влияния вы­сотного корректора на динамику полета в возмущенной атмос­фере рассмотрим поведение самолета с автопилотом без высот-

______ SqP2 + SiP____ Р[22] + h Р3 + Р2 + t$P + ^4

ного корректора, т. е. с законом управления (2.14). Объединяя уравнения (2.10) и (2.14), получаем следующие передаточные функции при воздействии горизонтальной составляющей ветра. Для угла тангажа *

J_ U0p* + Utp3 +• U2pl + иЗр g Т (р)

Для горизонтальной перегрузки

Для вертикальной перегрузки

W„ !w (р)=~ — = — — LроР* + ^Р3 + %/?, (3.30)

у *v g Tip) g Tip)

Для самолета с автопилотом без высотного корректора пере — Щцаточные функции при воздействии вертикальной составляющей ветра имеют следующий вид.

Для угла тангажа

Wb/V> (р)= —————— ШІ+JElL

^ Tip) Tip)

Для горизонтальной перегрузки

rv. L + (3 32,

* у g Т(р) g Т(р)

Для вертикальной перегрузки

W„ ,9 (p)=—Zl£L==±. уоР* + УіР3 + У2Р2 + узР /3 33)

> ’ g Т(Р) g і Т(р) к °°}

Амплитудно-частотные характеристики, построенные на осно­вании передаточных функций (3.28) —(3.33) для самолета № 1, приведены на рис. 3.1 (кривые 3 и 3′). В большем масштабе для «о начальные участки характеристик, относящихся к вертикаль­ному ветру, показаны на рис. 3.2 (кривые 3). Графики на рис. 3.2 свидетельствуют о том, что характеристики самолета с автопило­том без высотного корректора [закон (2.14)] идут в области ма­лых частот наиболее благоприятным образом. Что касается бо­лее высоких частот (рис. 3.1), то здесь различие между характе­

рне. 3.9. Переходные процессы самолета № 1 с автопилотом [закон (2.14)], полученные по полным уравнениям (2.10), при воздействии вертикального ветра

ристиками 2 и 3 незначительно. Особенно мало оно для вертикальных перегрузок (рис. 3.1,6), которые представляют наибольший практический интерес.

Переходные процессы при вертикальном порыве для самолета № 1 с автопилотом, закон управления которого выражается урав­нением (2.14), представлены на рис. 3.9 и 3.10. Переходные про­цессы на рис. 3.9 получены по полным уравнениям (2.10), а на рис. 3.10 — по упрощенным (2.11). Сравнение этих процессов по­казывает, что при исследовании поведения самолета с автопило­том без высотного корректора вполне допустимо использовать упрощенные уравнения самолета.

Характер переходных процессов весьма благоприятен, нет не­желательных выбросов угла атаки в область отрицательных значений. Все это подтверждает выводы, сделанные на основании частотных характеристик.

На рис. 3.11 приведены переходные процессы для самолета № 1 с автопилотом без высотного корректора, соответствующие входу самолета в попутный поток воздуха, имеющий скорость

Wx= Ю м/сек. Эти процессы получены на основании полных урав­нений (2.10). Характер переходных процессов позволяет утвер­ждать, что при отсутствии высотного корректора переход к но­вому установившемуся режиму происходит плавно и в сравни­тельно короткое время.

В заключение этого параграфа рассмотрим характеристики самолета с автопилотом со скоростной обратной связью, закон

Рис. ЗЛО. Переходные процессы самолета № 1 с автопило­том [закон (2Л4)], полученные по упрощенным уравнениям (2.11), при воздействии вертикального ветра

Рис. 3.11. Переходные процессы самолета № 1 с автопилотом без высот­ного корректора, полученные по полным уравнениям (2.10), при воздей­ствии горизонтального ветра

управления которого выражается уравнением (2.15). Объединяя

(2.15) с упрощенными уравнениями продольного движения

(2.11) , найдем передаточную функцию для вертикальной пере­грузки от вертикальной составляющей ветра

W„ ,9 (р)=-l-Zl£L=±. **Р’ + иР + ъ/Р + ъ. Р „ (3.34) у у g ф(р)- g Р* + Ті Р3 + ?2 Р2 + ЪР + П

Амплитудно-частотная характеристика самолета № 1, пост­роенная на основании (3.34), приведена на рис. 3.12 (кривая /).

При построении этой характеристики использовались, как и ра­нее, данные самолета № 1, приведенные в «Приложении А». Значения передаточных чисел U и сохранены теми же, что и в предыдущих примерах, а число г9=0,15 сек~х выбрано из усло­вия получения вполне удовлетво­рительного переходного процесса при отработке системой управля­ющего воздействия по углу тан­гажа.

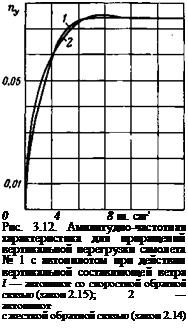Для сравнения на рис. 3.12 приведена частотная характерис­тика (кривая 2) самолета № 1 с автопилотом, имеющим закон уп­равления (2.14). Сравнение кри­вых 1 и 2 показывает, что система самолет — автопилот со скорост­ной обратной связью имеет прак­тически такую же амплитудно — частотную характеристику, что и система самолет — автопилот с жесткой обратной связью. Таким образом, автопилот со скоростной обратной связью не может дать каких-либо преимуществ при по­лете в турбулентной атмосфере.